國政流・逆枘の構造学的(構造力学的)な解析
要約すると、國政流逆枘の特異性と優位性は次の三点に集約される。
《1》 求心的構造
《2》 破壊力のベクトルに対して拘束力をもつ接合すべり面(分解不能なインターロック機構(構造)・外れない交差接合による組み手)
《3》 十分な実用耐久性を持つと同時に、組み上げ後は装飾性を一体化した美しい枘型が現れる。
《1》 は、次のように説明することができる。
「逆枘」は、互いの部材が45°の角度をもって組み立てられる。すなわち図1・実線のベクトルによってのみ組立が可能となる。角A及び角Cにおける組み立てベクトルは、点線のベクトルβとδにおきかえられる。すなわち「逆枘」で箱を組むということは、箱の中心Pに向かう力によって各部材が結合されるということになり、これを求心的構造と名付ける。この構造は、中心に向かって収束しているもの、外力によって破壊することはできないと、直感的に想像できる。
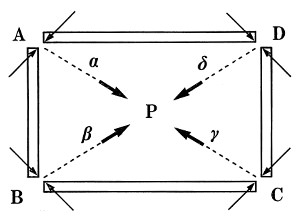
図1
このグローバルな直感は②のミクロ的な視点から証明することが可能である。一般的に、箱を破壊する力はf1、f2に示す如く、板材に垂直に働く力に代表される。この他に箱をひしゃげさせる破壊のパターンも考えられるが、これについては後述する。
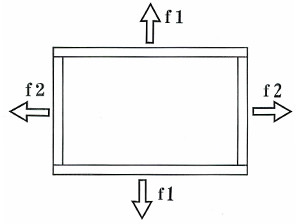
図2
逆枘は、45°方向に拘束力をもつすべり面が基本的なメカニズムになっているから、図2・f1、f2のように板材に垂直に働く力では破壊(分解)することはできない。「逆枘」を分解するには各コーナーに45°に働く分解ベクトル(図1 A〜Bのベクトルの逆)が存在しなければならず、このような分解ベクトルが箱の外部からの力(外力)によって生じることはなく、何故なら、部材に斜めに働く力は部材の表面にすべってしまうからである。(図3)
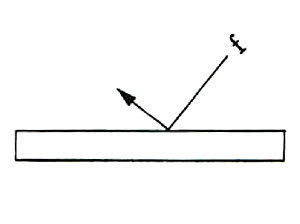
図3
次に、45°の分解ベクトルが発生する可能性を、箱の内部に働く力(内力)について検討してみたい。
そもそも箱に内力が働くという現象は、箱の中に物体が入っており、その状態で箱が移動した場合に生じる慣性力しかない。
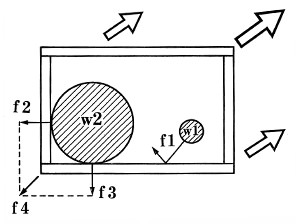
図4
その内力が、さらに45°の分解ベクトルを発生させるケースということは、箱が45°方向に移動した場合に限られる(図4)。その場合でも、例えばw1によって生じるf1という力は、箱の内面ですべってしまうので、分解ベクトルの原因となりえない。分解ベクトルの原因となりえるのは唯一w2のように箱のコーナーに物体がまたがっている場合である(f1とf3が同時に働くため、合力f3が発生し、これが角AとCに働く)。しかしながら、このケースに於いても、現実に45°の分解ベクトルが発生する可能性は限りなくゼロに近いといえる。何故なら、箱が厳密に45°の方向に移動する可能性はほとんど無いし、箱の寸法比率や物体の寸法形状によってf2、f3のバランスは様々な数値となるから、厳密に45°の分解ベクトルが一定時間あるいはくり返し発生する可能性はゼロである。厳密に45°の方向でなければ組めないものが、あいまいな角度の分解ベクトルで破壊されることは有りえない。
かくして、逆枘で組まれたこの箱は、外力、内力からのいづれでも破壊されないことが証明された。
この検証を、他の組み手について同様に行えば、逆枘の優位性はますます明らかになる。
ふつの組み手の場合は、いかなる方向の分解ベクトルでも破壊される(図5)。
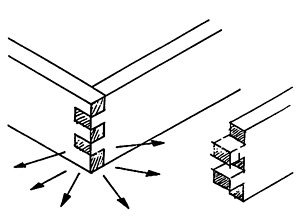
図5
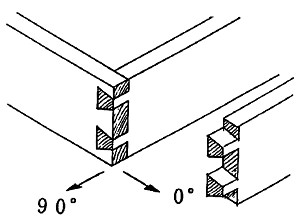
図6
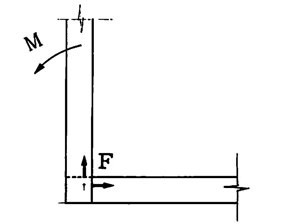
天秤(ダブルティルジョイント)は、ふつうの組み手よりは、遥かに有利だが、しかし90°方向の分解ベクトルに対しては無力である(図6)。さて、「枠体」をひしゃげる破壊のパターンも現実に存在するわけだが、これに対抗する各コーナーの強固さは、ミクロ的に見ればモーメントによって生じる力(右図F)にどれだけ耐えられるかという事になる。このFは0°又は90°に働くので、いずれの方向にも耐力をもつ逆枘が、やはり一番有利である(ふつうの組み手は、いかなる方向のベクトル耐力がないから、簡単にひしゃげてしまう)。
最後に、《2》について興味深い検討を加えてみよう。
箱を破壊する原因となる力のベクトルが0°又は90°であることは先に述べた(図2)。このベクトルが生じた場合に、組み手がどのように耐えるかということ、ふつうの組み手の場合は、接合すべり面の摩擦のみである。ダブルテイル場合は、90°以外の力に対しては接合すべり面が機械的拘束力をもつが、90°方向に対してはすべり面の摩擦のみである。
「逆枘」の場合はどうかというと、0°、90°いずれの方向に対しても接合すべり面が拘束力をもつ。すなわち、すべり面の摩擦は、箱の破壊に対抗する要素としては必要ないのである。別の言い方をすれば、ふつうの組み手あるいはダブルテイルと比べて小さい摩擦で組み立てられ、それでいて壊れにくいということになる。この事実は、すべり面が、その面対して一定の角度で働く拘束力をもつメカニズムの代表ともいえるネジ、ボルト類に類似しているといえる。ボルトは回せば進むが、軸方向に引き抜くことはできない。ふつうの組み手を摩擦力によってのみ固定されるクギにたとえれば、「逆枘」はボルトである。力の向きが違うから、締められるが外れないというメカニズムである。その意味では、もやい結索術にも類似している。いずれにせよ、人類の知恵としての共通のパターンがみられて、実に興味深いといえる。
箱体の破壊の原因となるものは、外力、内力の他に、部材(木材)の反りや曲がりによるものも考えられる。そのような反張による分解力は、0°又は90°にしか働かない。従って、この観点からも「逆枘」の優位性が認められる。長火鉢などは、中で火をたく道具であるから、構造部材に与える温度条件がきびしい。
きびしい温度条件のもとで、当然、大きな反張が起こる。それをビシッと押さえて分解を防ぐには、「逆枘」は最も適した組み手であると言える。逆に、長火鉢を丈夫に作るために開発された技術が「逆枘」と言うことができる。
もう一度まとめてみると、次のようになる。
逆枘で組んだ箱は、二辺方向に拘束力をもつ。
どの方向にも拘束力をもたない天秤と比べると、逆枘の構造的優位性は明らかである。また、二辺方向に拘束力ということは、求心的構造であり、繊維方向で四周を囲まれた箱として異方性をもたないということである。それ故、繊維に直交する方向に対しても、異方性をもたない。この性格は、反張、狂いなどの異方性を本質的に備えている木材を利用する上で極めて有利である。「求心的等方性」が「異方性」を封じ込めてしまうからである。
この國政流逆枘は、十分な実用耐久性を持つと同時に、組み上げ後は美しい枘型が現れる。構造強度・一度組み上げたら外せないインターロッキング機構と装飾性を一体化した独自の技法を完成させている。更に、外観フォルムは、一見どうやって組み立てるか判らないパズルのようなカラクリの性格帯び、遊び心も包含している。
この一連の組み手技法は、木という自然素材の特性・制約を最大限に活かした究極の木工ジョイントシステムであるということができるであろう。
(構造解析協力:大竹 收)20160203AQ



