Gyaku Hozo inversed tenons

Structural Analysis

In brief, the uniqueness and the advantages of Kunimasa inversed tenons (“gyaku hozo”) are based on the following three factors :

1. Centripetal structure

2. Joint slip plane’s resistance to destructive vectors (Once the joint has been assembled, it is impossible to disassemble it because of the interlock construction method and the crossing joints which can not be taken apart.)

3. Sufficient durability and beautiful design after assembly as ornamentation functions.

Factor  1  can be explained in the following way :

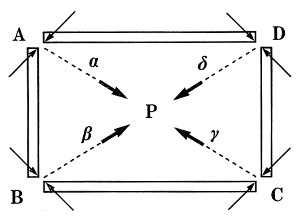
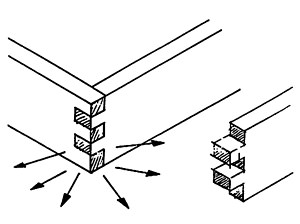
The “Gyaku Hozo inversed tenon” joints are assembled at 45 degree angles.

In other words, it is only possible to assemble them using the vectors shown with the lines in Figure 1.

The assembly vectors for corner A and corner C can be replaces by vector beta and vector delta indicates by the dotted lines in Figure 1.

(Figure 1)

In short, assembling a box with “Gyaku Hozo inversed tenons” means each piece is combined with a force in the direction of P, the center of the box. I call this a centripetal structure. Since this structure is directed toward the center, we can assume that this box can not be broken by forces from the outside.

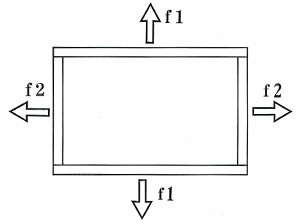
This “macro” assumption can be proved from a “micro” viewpoint of ➁ as well. In general, as shown with f1 and f2 in Figure 2, most forces capable of breaking the box are forces which operate on a perpendicular angle in relation to the boards.

(Figure 2)

A pattern of destruction in which the box is crushed is also conceivable. This situation will be discussed later.

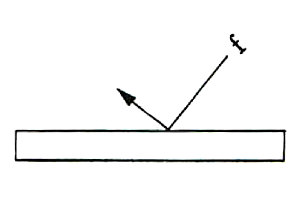
Since the basic mechanisms of “Gyaku Hozo inversed tenons” are the slip planes which are pulled together at 45 degree angles, inversed tenons can not be destroyed or disassembled by forces which affect boards at perpendicular angles as shown in f1 and f2 in Figure 2. In order to disassemble “Gyaku Hozo inversed tenons.” disassemblingvectors working at 45 degree angles must exist at each corner. (This is the opposite of the vectors on corners A and B shown in Figure 1). This kind of dissassembling vector can not occur through forces outside the box because forces working at diagonal angles will always slip on the surface of the wood pieces (Figure 3)

(Figure 3)

Next, let’s discuss the possibility of the occurrence of 45 degree angle disassembling vectors from the inside of the box.

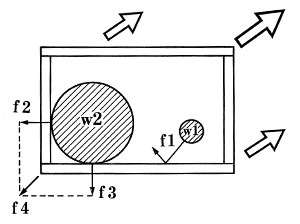
First of all, the phenomenon in which internal forces occur inside the box could only be inertia forces occurring due to the movement of objects inside the box. In addition, cases in which these internal forces create a 45 degree disassembling vector would be limited to only those cases in which the box moves at a 45 degree angle (Figure 4).

(Figure 4)

Even in cases such as these, for example, the force f1 in Figure 4 created by w1 would slip on the internal surface of the box and would not become the source of a disassembling vector. the only case in which this force would be able to become a disassembling force is that shown by w2 in Figure 4, in which the object comes in contact with both perpendicular surfaces of one corner. In this case, forces f2 and f3 occur at the same time and f4 will be created by these forces, so f4 impacts corners A and C. However, even in this case, the possibility of a 45 degree disassembly angle occurring is practically nonexistent. This is because, first, it is almost impossible that the box would move at exactly a 45 degree angle. In addition, the balance between f2 and f3 would be altered by the measurement ratio of the box and the size and shape of the object, and the possibility of disassembling vector of exactly 45 degree occurring over a certain period of time, or of it occurring repeatedly is nil. Finally, it is impossible that something which can only be assembled at exact 45 degree angles could be broken by disassembling vectors of ambiguous angles.

Using another assembly method in the same way, the advantages of inversed tenons become even more clear. With normal joints, boxes can be broken by disassembling vectors in any direction (Figure 5).

(Figure 5)

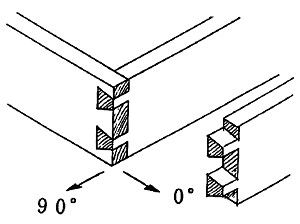
Though dovetail joints are far more advantageous than normal assembly, they are powerless in relation to disassembling vectors at 90 degree (Figure 6).

Patterns of “breaking “frame objects” are also conceivable, but, from a “micro”perspective, the strength of each opposite corner is a question of to what extent it is able to resist forces resulting from the momentum (see F in Figure 6).

(Figure 6)

This force F works at 0 or 90 degrees, so inversed tenons .. which are able to resist force from both of these directions- are the most advantageous joints. (With a normal assembly, as there is no resistance to vectors from any angle, the boxes can be easily broken).

FInally, I would like to add a discussion of the very interesting factor 2.

We have already discussed that the vectors of forces which are able to cause the destruction of the box are either 0 degrees or 90 degrees (Figure 2). For cases in which these sort of vectors occur, how well do the joints withstand these vectors? With normal joints, the only resistance against these forces is the joint slip plane friction.

With dovetails, the joint slip plane exhibits mechanical resistance to forces other than those at 90 degrees.

However, in response to forces at a direction of 90 degree, the only resistance is the slip plane friction.

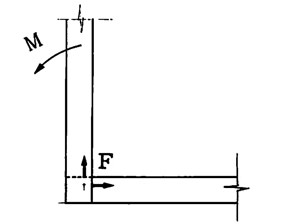
If “Gyaku Hozo inversed tenons” are used, the joint slip plane exhibits mechanical resistance against forces at both 0 degrees and 90 degrees. In other words, a slip plane frictional force is not necessary to protecting the box destruction. In addition, it can also be said that, in comparison to normal joints or dovetail joints, inversed tenon joints are assembled with less frictional force, yet they are hard to break. This is similar to screws and bolts which are the most typical example of mechanisms in which the slip plane has some sort of mechanical resistance acting on the plane at a certain angle. Bolts can be removes by unscrewing them, but it is impossible to pull them out at the same angle at which they were inserted. If we think of normal joints as nails which fix objects through the use of frictional force only. “Gyaku Hozo inversed tenons” can be thought of as bolts. Because the directions of the forces differ, this kind of joint can be tightened, but can be removed. In this sense, inversed tenons are also similar to knotting techniques such “Bowline knots.” In any case, it is very intriguing that this common pattern of human wisdom used in knotting and in joinery has been discovered.

(additional comments)

Possible causes of destruction of the box include external and internal forces as well as warping of the box pieces themselves. Disassembling forces caused by this kind of warping still work only at angles of 0 degree or 90 degrees. From this perspective, inversed tenons are still superior to normal joints.

As “hibachi” brasiers are devices in which fires burn, temperature conditions for structural materials are very exacting.

Under these strict conditions, significant warping occurs naturally. “Gyaku Hozo inversed tenons” are among the most suitable joints for controlling warping and disassembly of the box. We sometimes even think that the technology of “Gyaku Hozo inversed tenons” must have been developed in order to create colid, durable “hibachi” brasiers.

The following is a summary :

Boxes assembled with “Gyaku Hozo inversed tenons” exhibit resistant force toward two sides.

In comparison to dovetail joints which do not exhibit resistant force in any direction, it is clear that “Gyaku Hozo inversed tenons” are structurally superior. In addition, if a box exhibits resistant force to two sides, it is a centripetal structure. Even though boxes are structures which are made using four pieces of wood, and the grain of each piece of wood runs in its own direction, this centripetal structure does not allow the boxes to have irregularities. Thus, “Gyaku Hozo inversed tenons” do not have irregularities even when the grains cross at perpendicular angles. This characteristic is extremely advantageous when using wood materials which naturally possess irregularities such as warping and other imperfections. The reason for this is that the “centripetal uniformity” blocks the “irregularities.”

Kunimasa “Gyaku Hozo Inversed Tenons” are sufficiently durable and they also show their beautiful design after assembly. This unique technique can be described as encompassing structural strength, as interlock structure which can not be dissassembled, as well as ornamentation functions. Furthermore, the appearance of these inversed tenons also has “karakuri” characteristics which – in the same way a puzzle – one can not guess how they are assembled just by looking at them. Finally, this group of inversed tenons joint techniques can be called the absolutely finest wood joint system which makes maximize use of the special characteristics as well as of the limitations of wood as a natural material.

[Special thanks to Mr. Roger Griffith for proofreading the English translation.]